Mathematics
My area of mathematical interest is part of the field of analytic number theory. In particular I have investigated trace formulas and automorphic forms to
study the behavior of various spectral functions associated to degenerating families of Riemann surfaces.
For those not familiar with the field, A. Selberg introduced a trace formula in 1956. The Selberg trace formula resembles a lot the explicit formulas for the Riemann zeta function, that is the Selberg zeta function may be viewed as the analog to the Riemann zeta function. With such a resemblance, Selberg thought that this may be possibly lead to prove the Riemann hypothesis, that is possibly the most famous hypothesis in number theory.
What are automorphic forms, you may ask. They are functions that have "nice" properties; they are related to invariant operators, the Laplacian being the generator of all such. The Laplace operators is part of the heat equation as well as the wave equation. These equations describe how heat or sound spreads on a surface (for instance, the surface of a drum). The word spectral is related the the harmonics or resonances of these vibrations. The trace formula describes a relation between on the one hand the spectral inforamation encoded by the harmonics of a given surface and on the other hand the various geometric properties the surfaces posesses: its area, lengths of shortest paths, and singularities (i.e. cusps or conical ends).
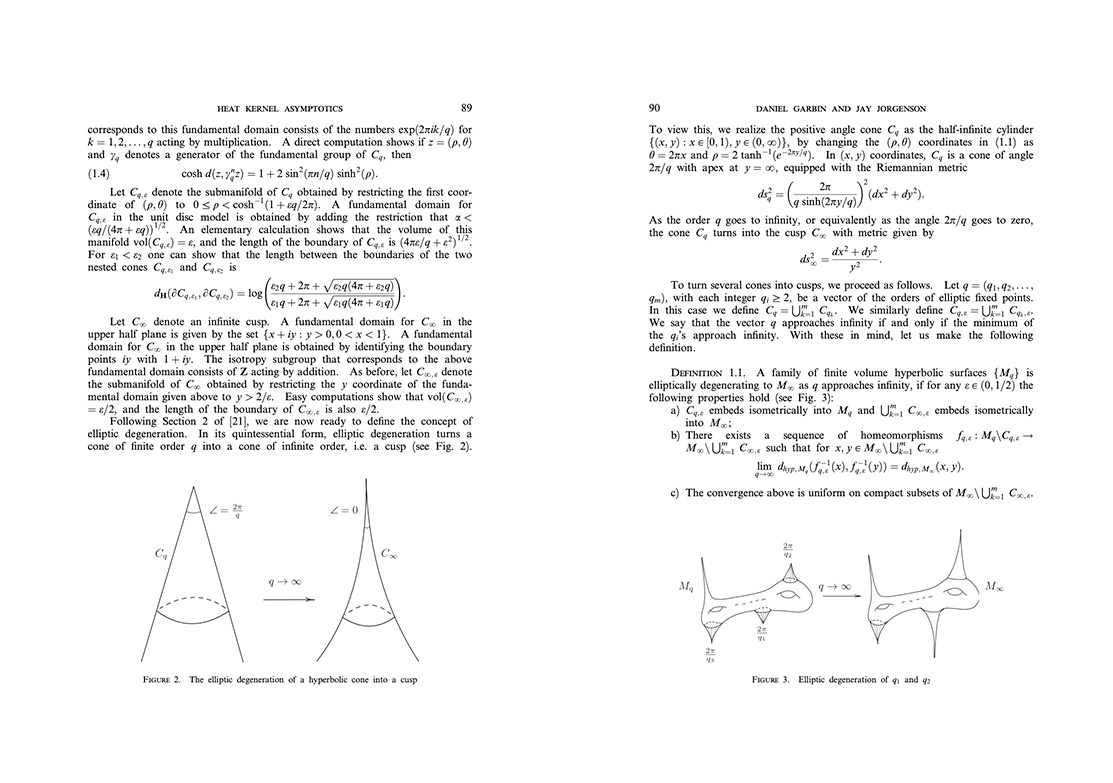
In my research I investigate the spectrum of the Laplace operator associated to hyperbolic Riemann surfaces, as well as various types of Eisenstein series, the Selberg zeta, spectral zeta, and other generalized zeta functions which are of special interest to number theorists. In the process, I have considered the behavior of such functions in the context of families of hyperbolic Riemann surfaces of finite volume, using heat kernel techniques.
In [GJM 08] we consider hyperbolically degenerating families of Riemann surfaces and show that if \(\gamma\) corresponds to a degenerating hyperbolic element, then a multiple of the associated hyperbolic Eisenstein series converges to a parabolic Eisenstein series on the limit surface, while in [GvP 09] we show the convergence up to a factor of the elliptic Eisentein series associated to a degenerating elliptic element to the parabolic Eisenstein series associated to the newly developed cusp on the limit surface.
For those not familiar with the field, A. Selberg introduced a trace formula in 1956. The Selberg trace formula resembles a lot the explicit formulas for the Riemann zeta function, that is the Selberg zeta function may be viewed as the analog to the Riemann zeta function. With such a resemblance, Selberg thought that this may be possibly lead to prove the Riemann hypothesis, that is possibly the most famous hypothesis in number theory.
What are automorphic forms, you may ask. They are functions that have "nice" properties; they are related to invariant operators, the Laplacian being the generator of all such. The Laplace operators is part of the heat equation as well as the wave equation. These equations describe how heat or sound spreads on a surface (for instance, the surface of a drum). The word spectral is related the the harmonics or resonances of these vibrations. The trace formula describes a relation between on the one hand the spectral inforamation encoded by the harmonics of a given surface and on the other hand the various geometric properties the surfaces posesses: its area, lengths of shortest paths, and singularities (i.e. cusps or conical ends).
In my research I investigate the spectrum of the Laplace operator associated to hyperbolic Riemann surfaces, as well as various types of Eisenstein series, the Selberg zeta, spectral zeta, and other generalized zeta functions which are of special interest to number theorists. In the process, I have considered the behavior of such functions in the context of families of hyperbolic Riemann surfaces of finite volume, using heat kernel techniques.
In [GJM 08] we consider hyperbolically degenerating families of Riemann surfaces and show that if \(\gamma\) corresponds to a degenerating hyperbolic element, then a multiple of the associated hyperbolic Eisenstein series converges to a parabolic Eisenstein series on the limit surface, while in [GvP 09] we show the convergence up to a factor of the elliptic Eisentein series associated to a degenerating elliptic element to the parabolic Eisenstein series associated to the newly developed cusp on the limit surface.
In [GJ 20] we study the spectral theory of the
Laplacian on elliptically degenerating families of Riemann
surfaces. By extending results from [JoLu 97a], [JoLu 97b], and [HJL 97] to the elliptic degeneration setting, we establish an asymptotic expansion for
the regularized heat trace in terms of the degeneration parameters. In [GJ 18], we make use of these results in order to
describe the behavior through elliptic degeneration of various functions
including spectral counting
functions, spectral zeta functions, Selberg zeta functions, determinants of the Laplacian, wave and resolvent kernels.
As part of current projects, I study the asympotitc behavior for families of Hilbert modular surfaces and families associated to \(\Gamma_0(N)\). By employing heat kernel techniques, I investigate the behavior of the spectral counting functions associated to surfaces formed from the congruence subgroups \(\Gamma_0(N)\), \(\Gamma_1(N)\), and \( \Gamma(N) \) as \(N\) runs off to infinity.
References
As part of current projects, I study the asympotitc behavior for families of Hilbert modular surfaces and families associated to \(\Gamma_0(N)\). By employing heat kernel techniques, I investigate the behavior of the spectral counting functions associated to surfaces formed from the congruence subgroups \(\Gamma_0(N)\), \(\Gamma_1(N)\), and \( \Gamma(N) \) as \(N\) runs off to infinity.
References
- [GJ 20] Garbin, D. and Jorgenson, J.: Heat kernel asymptotics on sequences of elliptically degenerating Riemann surfaces. Kodai Math. J. 43 (2020), 84–128
- [GJ 18] Garbin, D. and Jorgenson, J.: Spectral asymptotics on sequences of elliptically degenerating Riemann surfaces. L'Enseignement Mathématique, vol. 64 1-2 (2018)
- [GJM 08] GARBIN, D., JORGENSON, J., and MUNN, M.: On the appearance of Eisenstein series through degeneration. Comment. Math. Helv. 83 (2008) 701-721.
- [GvP 09] GARBIN, D., and VON PIPPICH, A.: On the behavior of Eisenstein series through elliptic degeneration. Commun. Math. Phys. 292 (2009) 511-528.